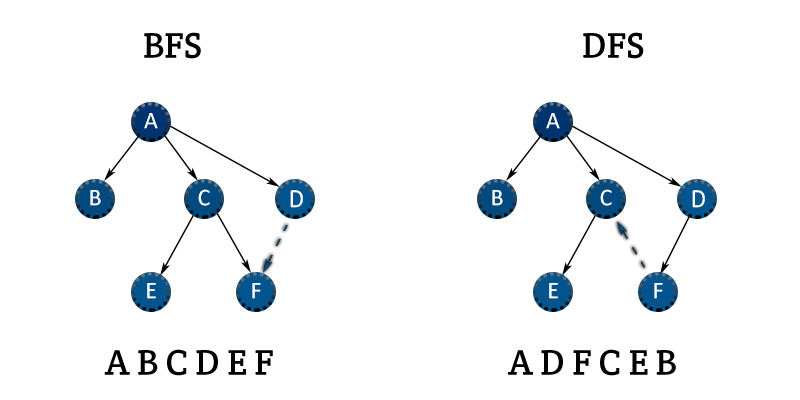
Ağaç veya graflarda arama işlemi yapan algoritmalardan bir tanesi olan BFS, geniş öncelikli arama yapmaktadır. Bu makalemizde BFS algoritması hakkında kısa bir bilgilendirme ve akabinde çalışma mantığına değinmeye çalışacağız.
BFS algoritmasında DFS algoritmasından farklı olarak derin arama yerin geniş arama yapılmaktadır. Temel farklardan bir tanesi ise kullanılan veri yapısıdır. BFS için literatürde yerini almış olan veri yapısı kuyruk veri yapısıdır. Kuyruk veri yapısı kullanan BFS’ de işlemler de FIFO (first in first out) yani ilk giren ilk çıkar prensibiyle çalışmaktadır.
BFS çalışma mantığı;
Bir başlangıç düğümü belirlenir ve tüm komşular ziyaret edilir. DFS’ den farklı olarak BFS’ de ziyaret edilen komşunun aynı anda gidilebilecek tüm komşuları aynı anda kuyruğa eklenir. DFS’ de hatırlayacağınız üzere bir komşudan sadece gidilebilecek bir diğer komşuya gidiliyor ve yığına ekleniyordu.
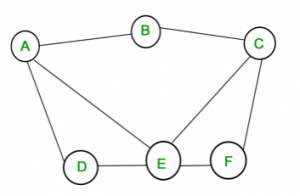
Resim-1
Yukarıdaki resimdeki örneği incelediğimizde başlangıç düğümü olarak A düğümünü belirlemiş olalım.
Öncelikle A düğümünden B ve D düğümüne aynı anda gidilebiliyor. Bu yüzden kuyruğa ilk başta A’ yı daha sonra B ve D’ yi ekliyoruz. İlk giren ilk çıkacağı için A çıkıyor B ve D giriyor.
Sonraki adımda B ve D’nin komşularına bakıyoruz C, E ve F olarak görülmektedir. Bu yüzden kuyruğa C, E ve F yi ekliyoruz. İlk giren ilk çıkacağından B yi çıkarıyoruz. Ardından D’yi çıkarıyoruz. Algoritmanın graf veya ağaç üzerinde dolaşma (traverse) işlemi bu şekilde kuyruk veri yapısı üzerinden ilerlemektedir.
Notlar;
Her adımda kuyruktan bir eleman çıkarılır. FIFO olduğu için ilk eleman ilk çıkar.
Bu algoritmada komşular ziyaret edilerek devam edildiği için bir adımda birden fazla komşu kuyruğa girebilir.
Özetle her adımda kuyruktaki en öndeki düğümün komşularına bakıyoruz ve kendisini çıkarıyoruz komşusunu kuyruğa ekliyoruz. Eğer kuyruktaki düğümün komşusu yoksa ilgili adımda kuyruktan sadece çıkarma yapıyoruz yani komşu olmadığı için ekleme yapmıyoruz.
BFS algoritmasının karmaşıklığını inceleyecek olursak her bir düğümü en az 1 kez gezdiği için O(N) olacaktır.
Bu konuyla ilgili sorularınızı alt kısımda bulunan yorumlar alanını kullanarak sorabilirsiniz.
Referanslar